Рождение Солнца.
Казалось бы о Солнечной системе известно многое всем, кто хотя бы иногда открывал в школе учебник астрономии. Но на самом деле наша галактика таит в себе огромное множество тайн и секретов, а новые факты о Солнечной системе, которые становятся известны учёным, способны удивить даже самых искушённых знатоков астрономии.
1. Скорость вращения 220-240 км/с
Солнечная система: скорость вращения 220-240 км/с.
В космосе движется все. Солнечная система вращается вокруг центра Галактики со скоростью 220-240 км/с, а на то, чтобы закончить один период обращения у нее уходит около 240 млн лет.
2. Солнечные затмения
Солнечная система: солнечное затмение на Земле.
Солнечные затмения можно наблюдать с любого места Солнечной системы. Но Земля — единственное место, где можно полюбоваться полным солнечным затмением.
3. Масса Солнца 99,86% от массы Сс
Солнечная система: масса Солнца составляет 99,86% от массы Сс.
Как известно, Солнце намного больше любой планеты в нашей системе. Об этом мало кто задумывается, но на самом деле масса Солнца составляет около 99,86% от общей массы Солнечной системы.
4. Скорость ветра до 2100 км/ч
Солнечная система: максимальная скорость ветра на Земле — 408 км/ч.
На Земле максимальная скорость ветра была зафиксирована на австралийском острове Барроу и составляла 408 км/ч. А самые сильные ветры в Солнечной системе дуют на Нептуне: до 2100 км/ч.
5. Химический состав
Солнечная система: химический состав.
В последнее время ученые разработали новую модель химического состава ранней Солнечной системы. Согласно этой теории, около половины воды, которая в настоящее время есть на Земле, появилась из межзвездного льда во время формирования Солнца.
6. Вода в Сс
Солнечная система: вода на Уране.
За последние пару десятков лет ученые установили, что на некоторых планетах и их спутниках в Солнечной системе есть вода в разных состояниях. Однако, Земля является единственным местом в Солнечной системе, где вода может присутствовать во всех трех состояниях: твердом, жидком и парообразном.
7. «Мертвый близнец»
Солнечная система: Венера — «мертвый близнец» Земли.
Из всех планет Солнечной системы, Венера считается близнецом Земли. Несмотря на то, что на ее поверхности условия вообще непригодны для жизни человека (к примеру, только температура составляет 464 ° C), она имеет примерно одинаковый размер и орбиту с Землей.
8. Нейтрино
Солнечная система: нейтрино и Сс.
В XX веке была открыта стабильная нейтральная элементарная частица нейтрино. Чтобы образно описать ее размеры, приведем следующее сравнение: если бы атом был размером с Солнечную систему, то нейтрино было бы размером с мяч для гольфа.
9. До -224 °C
Солнечная система: -224 °C на Уране.
Самая холодная же планетарная атмосфера в Солнечной системе — на Уране. Здесь температура опускается до -224 ° C.
10. Самая высокая гора в Сс
Солнечная система: самая высокая гора на Марсе.
Самая высокая горная вершина на Земле — Эверест (Джомолунгма), высота которой составляет 8 848 м. А самая высокая гора в Солнечной системе — на Марсе. Здесь высота горы Олимп составляет около 22 км.
11. Самая большая модель
Солнечная система: самая большая модель Солнца диаметром 110 метров.
В Швеции есть самая большая модель Солнечной системы в мире. Она сделана в масштабе 1:20 млн и простирается на 950 км.
12. Тройка лидеров
Солнечная система: Юпитер, Сатурн, Уран.
Уран является третьей по величине планеты в Солнечной системе. Первый по величине — Юпитер, а второй — Сатурн.
13. Самые большие бури
Солнечная система: пылевые бури Марса.
На Марсе также бушуют самые большие пылевые бури в Солнечной системе. Они зачастую длятся в течение нескольких месяцев и могут покрывать всю планету.
14. Орбитальная скорость Земли
Солнечная система: орбитальная скорость Земли.
Земля движется по орбите со скоростью около 108 000 км/ч.
15. Вулканы Венеры
Солнечная система: вулканы Венеры.
Согласно разным подсчетам, на Земле есть от 1 000 до 1 500 вулканов. А больше всего их в Солнечной системе на Венере — более 1 600.
16. Родом из облака
Солнечная система: родом из газопылевого облака.
Возраст Солнечной системы — 4,57 млрд лет. Именно тогда она сформировалась из газопылевого облака.
17. Солнечная гравитация
Солнечная система: солнечная гравитация.
Как известно, у Солнца намного более сильная гравитация. Человек, который весит 68 кг на Земле, весил бы на Солнце 1 905 кг.
18. Лунная гравитация
Солнечная система: лунная гравитация.
А теперь переместимся поближе к нашей планете. Тот же человек весом 68 кг весил бы 11 кг на Луне.
19. Гравитационные эффекты «невидимки»
Солнечная система: гравитационные эффекты «невидимки».
Ученые полагают, что в Солнечной системе далеко за орбитой Плутона есть девятая планета, которая примерно в 10 раз больше Земли. Ее до сих пор не смогли обнаружить, а ее существование предполагается из-за гравитационных эффектов, которые она оказывает на другие объекты.
20. Самые известные орбиты
Солнечная система: самые известные орбиты…
Гравитация — Википедия
Гравита́ция (притяже́ние, всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — универсальное фундаментальное взаимодействие между всеми материальными телами. В приближении малых (по сравнению со скоростью света) скоростей и слабого гравитационного взаимодействия описывается теорией тяготения Ньютона, в общем случае описывается общей теорией относительности Эйнштейна. В квантовом пределе гравитационное взаимодействие предположительно описывается квантовой теорией гравитации, которая ещё не разработана.
Гравитация играет крайне важную роль в структуре и эволюции Вселенной (устанавливая связь между плотностью Вселенной и скоростью её расширения)[1], определяя ключевые условия равновесия и устойчивости астрономических систем[2]. Без гравитации во Вселенной не было бы планет, звёзд, галактик, чёрных дыр[3]. Гравитационное сжатие является основным источником энергии на поздних стадиях эволюции звезд (белые карлики, нейтронные звезды, чёрные дыры).[4]
Согласно общей теории относительности, гравитационное взаимодействие является инвариантным относительно С-симметрии, P-симметрии и Т-симметрии [5]
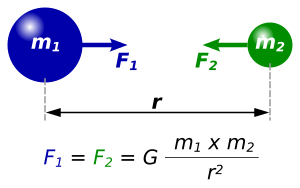 Закон всемирного тяготения
Закон всемирного тяготения
В рамках классической механики гравитационное притяжение описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m1{\displaystyle m_{1}} и m2{\displaystyle m_{2}}, разделёнными расстоянием r{\displaystyle r}, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния:
- F=Gm1m2r2.{\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}.}
Здесь G{\displaystyle G} — гравитационная постоянная, равная примерно 6,67⋅10−11 м³/(кг·с²)[6][7].
Этот закон выполняется в приближении при малых по сравнению со скоростью света v≪c{\displaystyle v\ll c} скоростей и слабого гравитационного взаимодействия (если для изучаемого объекта, расположенного на расстоянии R{\displaystyle R} от тела массой M{\displaystyle M}, величина GMc2R≪1{\displaystyle {\frac {GM}{c^{2}R}}\ll 1}[8]). В общем случае гравитация описывается общей теорией относительности Эйнштейна.
Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося также и при изучении излучений (см., например, Давление света), и являющегося прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.
Гравитационное поле, так же как и поле силы тяжести, потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность гравитационного поля влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в гравитационном поле часто существенно упрощает решение.
В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что, как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.
Большие космические объекты — планеты, звёзды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.
Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это, тем не менее, очень важная сила во Вселенной. В частности, электромагнитное взаимодействие между телами в космических масштабах мало, поскольку полный электрический заряд этих тел равен нулю (вещество в целом электрически нейтрально).
Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.
Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, чёрные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.
Гравитация была первым взаимодействием, описанным математической теорией. Аристотель (IV век до н. э.) считал, что объекты с разной массой падают с разной скоростью. И только много позже (1589 год) Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687 год) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.
Небесная механика и некоторые её задачи[править | править код]
Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации, называется небесной механикой.
Наиболее простой задачей небесной механики является гравитационное взаимодействие двух точечных или сферических тел в пустом пространстве. Эта задача в рамках классической механики решается аналитически в замкнутой форме; результат её решения часто формулируют в виде трёх законов Кеплера.
При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе эта неустойчивость не позволяет предсказать точно движение планет на масштабах, превышающих сотню миллионов лет.
В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: Солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — сложная структура колец Сатурна.
Несмотря на попытки точно описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.
В сильных гравитационных полях (а также при движении в гравитационном поле с релятивистскими скоростями) начинают проявляться эффекты общей теории относительности (ОТО):
Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого было подтверждено прямыми наблюдениями в 2015 году[9]. Однако и раньше были весомые косвенные свидетельства в пользу его существования, а именно: потери энергии в тесных двойных системах, содержащих компактные гравитирующие объекты (такие как нейтронные звезды или чёрные дыры), в частности, обнаруженные в 1979 году в знаменитой системе PSR B1913+16 (пульсаре Халса — Тейлора) — хорошо согласуются с моделью ОТО, в которой эта энергия уносится именно гравитационным излучением[10].
Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного n{\displaystyle n} -польного источника пропорциональна (v/c)2n+2{\displaystyle (v/c)^{2n+2}}, если мультиполь имеет электрический тип, и (v/c)2n+4{\displaystyle (v/c)^{2n+4}} — если мультиполь магнитного типа[11], где v{\displaystyle v} — характерная скорость движения источников в излучающей системе, а c{\displaystyle c} — скорость света в вакууме. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:
- L=15Gc5⟨d3Qijdt3d3Qijdt3⟩,{\displaystyle L={\frac {1}{5}}{\frac {G}{c^{5}}}\left\langle {\frac {d^{3}Q_{ij}}{dt^{3}}}{\frac {d^{3}Q^{ij}}{dt^{3}}}\right\rangle ,}
где Qij{\displaystyle Q_{ij}} — тензор квадрупольного момента распределения масс излучающей системы. Константа Gc5=2,76⋅10−53{\displaystyle {\frac {G}{c^{5}}}=2{,}76\cdot 10^{-53}} (1/Вт) позволяет оценить порядок величины мощности излучения.
Начиная с 1969 года (эксперименты Вебера (англ.)), создаются детекторы гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (LIGO, VIRGO, TAMA (англ.), GEO 600), а также проект космического гравитационного детектора LISA (Laser Interferometer Space Antenna — лазерно-интерферометрическая космическая антенна). Наземный детектор в России разрабатывается в Научном центре гравитационно-волновых исследований «Дулкын»[12] республики Татарстан.
Измерение кривизны пространства на орбите Земли (рисунок художника)
Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и поэтому их обнаружение и экспериментальная проверка весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.
Среди них, в частности, можно назвать увлечение инерциальных систем отсчёта (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли. Обработка полученных данных велась до мая 2011 года и подтвердила существование и величину эффектов геодезической прецессии и увлечения инерциальных систем отсчёта, хотя и с точностью, несколько меньшей изначально предполагавшейся.
После интенсивной работы по анализу и извлечению помех измерений, окончательные итоги миссии были объявлены на пресс-конференции по NASA-TV 4 мая 2011 года и опубликованы в Physical Review Letters[13]. Измеренная величина геодезической прецессии составила −6601,8±18,3 миллисекунды дуги в год, а эффекта увлечения — −37,2±7,2 миллисекунды дуги в год (ср. с теоретическими значениями −6606,1 mas/год и −39,2 mas/год).
В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.
Существует современная каноническая[14] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой. Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.
Общая теория относительности[править | править код]
В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала), иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем — метрикой четырёхмерного пространства-времени, а напряжённость гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой.
Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих геометрические свойства пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырёхмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием её формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка.
Известно, что в ОТО имеются затруднения в связи с неинвариантностью энергии гравитационного поля, поскольку данная энергия не описывается тензором и может быть теоретически определена разными способами. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия (так как спин протяжённого объекта также не имеет однозначного определения). Считается, что существуют определённые проблемы с однозначностью результатов и обоснованием непротиворечивости (проблема гравитационных сингулярностей).
Однако экспериментально ОТО подтверждается до самого последнего времени (2012 год). Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое только и доступно сейчас экспериментальной проверке.
Теория Эйнштейна — Картана[править | править код]
Теория Эйнштейна — Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время, кроме энергии-импульса, также и спина объектов[15]. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса: один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением; второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения.
Получаемые поправки к ОТО, в условиях современной Вселенной, настолько малы, что пока не видно даже гипотетических путей для их измерения.
Теория Бранса — Дикке[править | править код]
В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ (Релятивистская теория гравитации), относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум группам уравнений для компонент гравитационного поля: одна для метрики, вторая — для скалярного поля. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля[16].
Подобное распадение уравнений на два класса имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского[17]. Благодаря наличию безразмерного параметра в теории Йордана — Бранса — Дикке появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов. При этом при стремлении параметра к бесконечности предсказания теории становятся всё более близкими к ОТО, так что опровергнуть теорию Йордана — Бранса — Дикке невозможно никаким экспериментом, подтверждающим общую теорию относительности.
Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена общепризнанная непротиворечивая квантовая теория. При низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2. Однако получающаяся теория неперенормируема, и поэтому считается неудовлетворительной.
В последние десятилетия разработаны несколько перспективных подходов к решению задачи квантования гравитации: теория струн, петлевая квантовая гравитация и прочие.
- Теория струн
В ней вместо частиц и фонового пространства-времени выступают струны и их многомерные аналоги — браны. Для многомерных задач браны являются многомерными частицами, но с точки зрения частиц, движущихся внутри этих бран, они являются пространственно-временными структурами. Вариантом теории струн является М-теория.
- Петлевая квантовая гравитация
В ней делается попытка сформулировать квантовую теорию поля без привязки к пространственно-временному фону, пространство и время по этой теории состоят из дискретных частей. Эти маленькие квантовые ячейки пространства определённым способом соединены друг с другом, так что на малых масштабах времени и длины они создают пёструю, дискретную структуру пространства, а на больших масштабах плавно переходят в непрерывное гладкое пространство-время. Хотя многие космологические модели могут описать поведение вселенной только от Планковского времени после Большого Взрыва, петлевая квантовая гравитация может описать сам процесс взрыва, и даже заглянуть раньше. Петлевая квантовая гравитация позволяет описать все частицы стандартной модели, не требуя для объяснения их масс введения бозона Хиггса.
- Причинная динамическая триангуляция
Причинная динамическая триангуляция — пространственно-временное многообразие в ней строится из элементарных евклидовых симплексов (треугольник, тетраэдр, пентахор) размеров порядка планковских с учётом принципа причинности. Четырёхмерность и псевдоевклидовость пространства-времени в макроскопических масштабах в ней не постулируются, а являются следствием теории.
Гравитация в микромире при низких энергиях элементарных частиц на много порядков слабее остальных фундаментальных взаимодействий. Так, отношение силы гравитационного взаимодействия двух покоящихся протонов к силе электростатического взаимодействия равно 10−36{\displaystyle 10^{-36}}.
Для сравнения закона всемирного тяготения с законом Кулона величину GNm{\displaystyle {\sqrt {G_{N}}}m} называют гравитационным зарядом. В силу принципа эквивалентности массы и энергии гравитационный заряд равен GNEc2{\displaystyle {\sqrt {G_{N}}}{\frac {E}{c^{2}}}}. Гравитационное взаимодействие становится равным по силе электромагнитному, когда гравитационный заряд равен электрическому GNEc2=e{\displaystyle {\sqrt {G_{N}}}{\frac {E}{c^{2}}}=e}, то есть при энергиях E=ec2GN=1018{\displaystyle E={\frac {ec^{2}}{\sqrt {G_{N}}}}=10^{18}} ГэВ, пока недостижимых на ускорителях элементарных частиц.[18][19]
Предполагается, что гравитационное взаимодействие было таким же сильным, как и остальные взаимодействия в первые 10−43{\displaystyle 10^{-43}} секунд после Большого взрыва[20].
- ↑ Вайнберг С. Первые три минуты. — М.: Энергоиздат, 1981. — С. 135.
- ↑ Нарликар Дж. Неистовая вселенная. — М.: Мир, 1985. — С. 25. — Тираж 100 000 экз.
- ↑ Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 144. — Тираж 50 000 экз.
- ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 311.
- ↑ В. Паули Нарушение зеркальной симметрии в законах атомной физики // Теоретическая физика 20 века. Памяти Вольфганга Паули. — М., ИЛ, 1962. — c. 383
- ↑ Improved Determination of G Using Two Methods // Phys. Rev. Lett. 111, 101102 (2013), DOI:10.1103/PhysRevLett.111.101102
- ↑ G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, G. M. Tino. Precision measurement of the Newtonian gravitational constant using cold atoms (неопр.). Nature (18 June 2014).
- ↑ Нарликар Дж. Неистовая вселенная. — М.: Мир, 1985. — С. 70. — Тираж 100 000 экз.
- ↑ LIGO Scientific Collaboration and Virgo Collaboration, B. P. Abbott, R. Abbott, T. D. Abbott, M. R. Abernathy. Observation of Gravitational Waves from a Binary Black Hole Merger // Physical Review Letters. — 2016-02-11. — Т. 116, вып. 6. — С. 061102. — doi:10.1103/PhysRevLett.116.061102.
- ↑ Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 87. — Тираж 50 000 экз.
- ↑ См. аналогию между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм.
- ↑ Научный Центр Гравитационно-Волновых Исследований «Дулкын» Архивная копия от 25 сентября 2006 на Wayback Machine
- ↑ C. W. F. Everitt et al. Gravity Probe B: Final results of a space experiment to test general relativity, Physical Review Letters (1 мая 2011). Дата обращения 6 мая 2011.
- ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
- ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А. Калибровочная теория гравитации. — М.: Изд. МГУ, 1985.
- ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
- ↑ С ортодоксальной точки зрения это уравнение представляет собой координатное условие.
- ↑ Яворский Б. М., Детлаф А. А., Лебедев А. К. Справочник по физике для инженеров и студентов вузов. — М.: Оникс, 2007. — С. 948. — ISBN 978-5-488-01248-6 — Тираж 5100 экз.
- ↑ Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 145. — Тираж 50 000 экз.
- ↑ Вайнберг С. Первые три минуты. — М.: Энергоиздат, 1981. — С. 136.
- Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). — М.: Наука, 1981. — 352c.
- Визгин В. П. Единые теории в 1-й трети XX в. — М.: Наука, 1985. — 304c.
- Иваненко Д. Д., Сарданашвили Г. А. Гравитация. 3-е изд. — М.: УРСС, 2008. — 200с.
- Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977.
- Торн К. Черные дыры и складки времени. Дерзкое наследие Эйнштейна. — М.: Государственное издательство физико-математической литературы, 2009.
Поверхностная гравитация — Википедия
Поверхностная гравитация (англ. surface gravity) — ускорение свободного падения, испытываемое на поверхности астрономического или иного объекта. Поверхностную гравитацию можно рассматривать как ускорение вследствие притяжения, испытываемое гипотетической пробной частицей, находящейся вблизи поверхности объекта и обладающей пренебрежимо малой массой, чтобы не вносить возмущения.
Поверхностная гравитация измеряется в единицах ускорения, которые в системе СИ равны м/с2. Иногда её удобно выражать в единицах земного ускорения свободного падения g = 9,80665 м/с2.[1] В астрофизике поверхностную гравитацию иногда выражают в виде lg g, который представляет собой десятичный логарифм от значения ускорения, выраженного в системе единиц СГС, в которой ускорение измеряется в см/с2.[2] Следовательно, поверхностная гравитация Земли в системе СГС равна 980,665 см/с2, а десятичный логарифм этой величины равен 2,992.
Гравитация на поверхности белого карлика очень сильна, а для нейтронных звёзд она ещё сильнее. Компактность нейтронной звезды приводит к тому, что для неё поверхностная гравитация составляет около 7·1012 м/с2, типичные значения имеют порядок 1012 м/с2, что в 100 000 000 000 раз превышает значение земной поверхностной гравитации. При этом скорость убегания с поверхности нейтронной звезды имеет порядок 105 км/с (треть скорости света).
Масса, радиус и поверхностная гравитация[править | править код]
| Название | Поверхностная гравитация |
|---|---|
| Солнце | 28,02g |
| Меркурий | 0,38g |
| Венера | 0,904g |
| Земля | 1,00g |
| Луна | 0,1654g |
| Марс | 0,376g |
| Фобос | 0,0005814g |
| Деймос | 0,000306g |
| Церера | 0,0275g |
| Юпитер | 2,53g |
| Ио | 0,183g |
| Европа | 0,134g |
| Ганимед | 0,15g |
| Каллисто | 0,126g |
| Сатурн | 1,07g |
| Титан | 0,14g |
| Энцелад | 0,0113g |
| Уран | 0,89g |
| Нептун | 1,14g |
| Тритон | 0,0797g |
| Плутон | 0,067g |
| Эрида | 0,0677g |
| 67P-CG | 0,000017g |
В теории гравитации Ньютона сила притяжения, создаваемая объектом, пропорциональна его массе: объект с вдвое большей массой создаёт вдвое большую силу. Сила притяжения в теории Ньютона обратно пропорциональна квадрату расстояния, поэтому удалившийся на вдвое большее расстояние объект создаёт в четыре раза меньшую силу. По аналогичному закону изменяется с расстоянием освещённость, создаваемая точечным источником.
Крупный объект, такой как планета или звезда, обычно имеет круглую форму вследствие достижения гидростатического равновесия (все точки на поверхности обладают одинаковой гравитационной потенциальной энергией). На малых масштабах более высокие области подвергаются эрозии, а осыпающееся вещество откладывается на более низких областях. На больших масштабах планета или звезда целиком деформируется до момента достижения равновесия.[4] Для большинства небесных тел результатом является то, что рассматриваемую планету или звезду можно считать почти идеальной сферой в случае малой скорости вращения. Для молодых массивных звёзд экваториальная скорость вращения может достигать 200 км/с и более, что может приводить к значительной сплюснутости. Примерами таких быстро вращающихся звёзд являются Ахернар, Альтаир, Регул A и Вега.
Тот факт, что многие крупные небесные тела имеют почти шарообразную форму, позволяет относительно несложно вычислять их поверхностную гравитацию. Сила притяжения вне сферически симметричного тела равна силе притяжения точечного тела той же массы, помещённого в центр исходного тела, что было доказано И. Ньютоном.[5] Следовательно, поверхностная гравитация планеты или звезды данной массы примерно обратно пропорциональна квадрату радиуса, а поверхностная гравитация планеты или звезды с заданной средней плотностью приблизительно пропорциональна радиусу. Например, недавно открытая планета Глизе 581 c превосходит Землю по массе в 5 раз, но маловероятно, что поверхностная гравитация также в 5 раз превосходит земную. Если масса данной планеты превосходит земную не более, чем в 5 раз[6] и планета является каменистой с крупным железным ядром, то её радиус примерно на 50% больше земного.[7][8] Гравитация на подобной планете приблизительно в 2,2 раза будет превышать земную. Если же планета ледяная или водная, то радиус вдвое может превышать радиус Земли, вследствие чего гравитация на поверхности превысит земную не более чем в 1,25 раза.[8]
Указанные выше пропорциональности можно выразить формулой
- g=mr2,{\displaystyle g={\frac {m}{r^{2}}},}
где g равно поверхностной гравитации, выраженной в единицах ускорения свободного падения для поверхности Земли, m равно массе объекта в единицах массы Земли (5,976·1024 кг), r равно радиусу объекта, выраженному в единицах среднего радиуса Земли (6371 км).[9] Например, Марс имеет массу 6,4185·1023 кг = 0,107 массы Земли и средний радиус 3390 км = 0,532 радиуса Земли.[10] Тогда поверхностная гравитация Марса равна
- 0,1070,5322=0,38{\displaystyle {\frac {0,107}{0,532^{2}}}=0,38}
в единицах значения для Земли. Если не использовать Землю в качестве тела отсчёта, то поверхностную гравитацию можно определять напрямую из закона всемирного тяготения:
- g=GMr2,{\displaystyle g={\frac {GM}{r^{2}}},}
где M — масса объекта, r — его радиус, G — гравитационная постоянная. Если ρ = M/V показывает среднюю плотность объекта, то выражение можно переписать в виде
- g=4π3Gρr,{\displaystyle g={\frac {4\pi }{3}}G\rho r,}
поэтому для фиксированной средней плотности поверхностная гравитация g пропорциональна радиусу r.
Поскольку гравитация обратно пропорциональна квадрату расстояния, то космическая станция на высоте 400 км над поверхностью Земли испытывает почти такую же силу притяжения, как и мы на поверхности Земли. Причина, по которой космическая станция не падает на землю, состоит не в том, что на неё не действует притяжение, а в том, что станция находится на орбите в свободном падении.
Объекты, не являющиеся сферически-симметричными[править | править код]
Большинство астрономических объектов не являются абсолютно сферически-симметричными. Одной из причин является то, что данные объекты обычно вращаются, то есть на их форму оказывают совместное влияние сила притяжения и центробежная сила, вследствие чего звёзды и планеты приобретают сплюснутую форму. На экваторе при этом поверхностная гравитация будет меньше, чем на полюсе. Данное явление использовал Хол Клемент в новелле «Экспедиция „Тяготение“», в которой упоминается массивная быстро вращающаяся планета, на которой гравитация на полюсах значительно превышала гравитацию на экваторе.
Поскольку распределение внутреннего вещества объекта может отклоняться от симметричной модели, то мы можем использовать поверхностную гравитацию для получения сведений о внутреннем строении объекта. В 1915-1916 годах на основе данного вывода по методу Лоранда Этвёша осуществлялся поиск нефти около города Гбелы в Словакии.[11], стр. 1663;[12], стр. 223. В 1924 году аналогичный метод использовался для уточнения положения нефтяных полей Nash Dome в Техасе.[12], стр. 223.
Иногда полезно вычислять поверхностную гравитацию простых гипотетических объектов, которые не встречаются в природе. Поверхностная гравитация бесконечных плоскостей, трубок, тонких оболочек и других нереалистичных фигур может использоваться при построении моделей гравитации реальных объектов.
Поверхностная гравитация чёрной дыры[править | править код]
В теории относительности ньютоновское понятие ускорения перестаёт быть чётко определённым. Для чёрной дыры поверхностную гравитацию нельзя определить как ускорение, испытываемое пробным телом на поверхности объекта, поскольку на горизонте событий ускорение стремится к бесконечности. Обычно используется понятие местного собственного ускорения (стремится к бесконечности вблизи горизонта событий), умноженного на коэффициент, связанный с гравитационным замедлением времени (стремится к нулю вблизи горизонта событий).
При рассмотрении поверхностной гравитации чёрной дыры следует определить понятие, аналогичное случаю ньютоновской поверхностной гравитации. Гравитация на поверхности чёрной дыры в общем случае определяется плохо. Можно определить поверхностную гравитацию для чёрной дыры, горизонт событий которой является горизонтом Киллинга.
Для случая статического горизонта Киллинга поверхностная гравитация κ{\displaystyle \kappa } представляет собой ускорение, необходимое для удержания объекта на горизонте событий. Если ka{\displaystyle k^{a}} представляет нормированный вектор Киллинга, то поверхностная гравитация определяется как
- ka∇akb=κkb,{\displaystyle k^{a}\,\nabla _{a}k^{b}=\kappa k^{b},}
уравнение записывается для горизонта. Для статичного и асимптотически плоского пространства-времени нормализацию следует выбирать так, чтобы kaka→−1{\displaystyle k^{a}k_{a}\rightarrow -1} при r→∞{\displaystyle r\rightarrow \infty }, а также κ≥0{\displaystyle \kappa \geq 0}.
Для решения Шварцшильда мы принимаем такое ka{\displaystyle k^{a}}, что ka∂a=∂∂t{\displaystyle k^{a}\partial _{a}={\frac {\partial }{\partial t}}}, для решения Керра — Ньюмена мы принимаем ka∂a=∂∂t+Ω∂∂φ{\displaystyle k^{a}\partial _{a}={\frac {\partial }{\partial t}}+\Omega {\frac {\partial }{\partial \varphi }}}, где Ω{\displaystyle \Omega } показывает угловую скорость.
Решение Шварцшильда[править | править код]
Поскольку ka{\displaystyle k^{a}} является вектором Киллинга, то ka∇akb=κkb{\displaystyle k^{a}\,\nabla _{a}k^{b}=\kappa k^{b}} соответствует −ka∇bka=κkb{\displaystyle -k^{a}\,\nabla ^{b}k_{a}=\kappa k^{b}}. В координатах (t,r,θ,φ){\displaystyle (t,r,\theta ,\varphi )} ka=(1,0,0,0){\displaystyle k^{a}=(1,0,0,0)}. Переход к системе координат Эддингтона-Финкельштейна v=t+r+2Mln|r−2M|{\displaystyle v=t+r+2M\ln |r-2M|} приводит к виду метрики
- ds2=−(1−2Mr)dv2+2dvdr+r2(dθ2+sin2θdφ2).{\displaystyle ds^{2}=-\left(1-{\frac {2M}{r}}\right)\,dv^{2}+2\,dv\,dr+r^{2}\left(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}\right).}
В общем случае изменения системы координат вектор Киллинга преобразуется как kv=Atvkt{\displaystyle k^{v}=A_{t}^{v}k^{t}}, что даёт вектора s ka′=(1,0,0,0){\displaystyle k^{a’}=(1,0,0,0)} и ka′=(−1+2Mr,1,0,0).{\displaystyle k_{a’}=\left(-1+{\frac {2M}{r}},1,0,0\right).}
Если b = v для ka∇akb=κkb{\displaystyle k^{a}\,\nabla _{a}k^{b}=\kappa k^{b}}, то получаем дифференциальное уравнение −12∂∂r(−1+2Mr)=κ.{\displaystyle -{\frac {1}{2}}{\frac {\partial }{\partial r}}\left(-1+{\frac {2M}{r}}\right)=\kappa .}
Следовательно, поверхностная гравитация для решения Шварцшильда при массе M{\displaystyle M} равна κ=14M.{\displaystyle \kappa ={\frac {1}{4M}}.}[13]
Решение Керра[править | править код]
Поверхностная гравитация для незаряженной вращающейся чёрной дыры равна
- κ=g−k,{\displaystyle \kappa =g-k,}
где g=14M{\displaystyle g={\frac {1}{4M}}} является поверхностной гравитацией решения Шварцшильда, k:=MΩ+2{\displaystyle k:=M\Omega _{+}^{2}}, Ω+{\displaystyle \Omega _{+}} равна угловой скорости у горизонта событий. Данное выражение приводит к температуре Хокинга 2πT=g−k{\displaystyle 2\pi T=g-k}.[14]
Решение Керра — Ньюмена[править | править код]
Поверхностная гравитация для решения Керра — Ньюмена равна
- κ=r+−r−2(r+2+a2)=M2−Q2−J2/M22M2−Q2+2MM2−Q2−J2/M2,{\displaystyle \kappa ={\frac {r_{+}-r_{-}}{2(r_{+}^{2}+a^{2})}}={\frac {\sqrt {M^{2}-Q^{2}-J^{2}/M^{2}}}{2M^{2}-Q^{2}+2M{\sqrt {M^{2}-Q^{2}-J^{2}/M^{2}}}}},}
где Q{\displaystyle Q} — электрический заряд, J{\displaystyle J} — угловой момент, r±:=M±M2−Q2−J2/M2{\displaystyle r_{\pm }:=M\pm {\sqrt {M^{2}-Q^{2}-J^{2}/M^{2}}}} — расположение двух горизонтов, a:=J/M{\displaystyle a:=J/M}.
Динамические чёрные дыры[править | править код]
Поверхностная гравитация для стационарных чёрных дыр определяется, поскольку все стационарные чёрные дыры обладают горизонтом Киллинга.[15] Недавно были предприняты попытки определения поверхностной гравитации динамических чёрных дыр, чьё пространство-время не является полем Киллинга.[16] На протяжении нескольких лет различными авторами предлагались разные варианты определения. На настоящий момент нет окончательного решения о справедливости каких-либо из определений.[17]
- ↑ p. 29, The International System of Units (SI), ed. Barry N. Taylor, NIST Special Publication 330, 2001.
- ↑ Smalley, B. The Determination of Teff and log g for B to G stars (неопр.). Keele University (13 июля 2006). Дата обращения 31 мая 2007.
- ↑ Isaac Asimov. The Collapsing Universe (неопр.). — Corgi, 1978. — С. 44. — ISBN 0-552-10884-7.
- ↑ Why is the Earth round?, at Ask A Scientist, accessed online May 27, 2007.
- ↑ Book I, §XII, pp. 218–226, Newton’s Principia: The Mathematical Principles of Natural Philosophy, Sir Isaac Newton, tr. Andrew Motte, ed. N. W. Chittenden. New York: Daniel Adee, 1848. First American edition.
- ↑ Astronomers Find First Earth-like Planet in Habitable Zone Архивировано 17 июня 2009 года., ESO 22/07, press release from the European Southern Observatory, April 25, 2007
- ↑ The HARPS search for southern extra-solar planets XI. Super-Earths (5 & 8 M_Earth) in a 3-planet system, S. Udry, X. Bonfils), X. Delfosse, T. Forveille, M. Mayor, C. Perrier, F. Bouchy, C. Lovis, F. Pepe, D. Queloz, and J.-L. Bertaux. arXiv:astro-ph/0704.3841.
- ↑ 1 2 Detailed Models of super-Earths: How well can we infer bulk properties?, Diana Valencia, Dimitar D. Sasselov, and Richard J. O’Connell, arXiv:astro-ph/0704.3454.
- ↑ 2.7.4 Physical properties of the Earth Архивная копия от 28 марта 2015 на Wayback Machine, web page, accessed on line May 27, 2007.
- ↑ Mars Fact Sheet, web page at NASA NSSDC, accessed May 27, 2007.
- ↑ Ellipsoid, geoid, gravity, geodesy, and geophysics Архивировано 28 августа 2003 года., Xiong Li and Hans-Jürgen Götze, Geophysics, 66, #6 (November–December 2001), pp. 1660–1668. DOI 10.1190/1.1487109.
- ↑ 1 2 Prediction by Eötvös’ torsion balance data in Hungary Архивировано 28 ноября 2007 года., Gyula Tóth, Periodica Polytechnica Ser. Civ. Eng. 46, #2 (2002), pp. 221–229.
- ↑ Raine, Derek J.; Thomas, Edwin George. Black Holes: An Introduction (неопр.). — illustrated. — Imperial College Press, 2010. — С. 44. — ISBN 1-84816-382-7. Extract of page 44
- ↑ Good, Michael; Yen Chin Ong. Are Black Holes Springlike? (англ.) // Physical Review D : journal. — 2015. — February (vol. 91, no. 4). — P. 044031. — doi:10.1103/PhysRevD.91.044031. — Bibcode: 2015PhRvD..91d4031G. — arXiv:1412.5432.
- ↑ Wald, Robert. General Relativity (неопр.). — University Of Chicago Press (англ.)русск., 1984. — ISBN 978-0-226-87033-5.
- ↑ Nielsen, Alex; Yoon. Dynamical Surface Gravity (англ.) // Classical Quantum Gravity : journal. — 2008. — Vol. 25.
- ↑ Pielahn, Mathias; G. Kunstatter; A. B. Nielsen. Dynamical surface gravity in spherically symmetric black hole formation (англ.) // Physical Review D : journal. — 2011. — November (vol. 84, no. 10). — P. 104008(11). — doi:10.1103/PhysRevD.84.104008. — Bibcode: 2011PhRvD..84j4008P. — arXiv:1103.0750.
Что такое гравитация и как она работает?

Латинское слово gravitas означает вес и дает нам слово «гравитация», которое является силой, которая дает объектам их вес. Это также корень слова «гравитировать», которое описывает то, что делает гравитация: заставляет объекты притягиваться друг к другу. Это то, что удерживает людей на Земле и держит Землю на своем месте в Солнечной системе. Хотя древние философы задавались вопросом, почему объекты падали столетия назад, у ученых до сих пор остаются вопросы о том, как действует гравитация и сегодня.
Что такое гравитация?

Проще говоря, гравитация — это сила, которая притягивает два тела друг к другу. Все, что имеет материю, то есть все, к чему можно прикоснуться, имеет гравитационное притяжение. Это включает в себя яблоки, людей и Землю. Несмотря на термин невесомость, невозможно избежать гравитационных сил. Космонавты все еще подвержены воздействию гравитации, но они движутся так быстро, что не приближаются к центру планеты и находятся в постоянном состоянии свободного падения.
Гравитация, масса и расстояние

Степень гравитации любого объекта пропорциональна массе объекта. Объекты с большей массой имеют большую гравитацию. Поскольку Земля является самым крупным и ближайшим объектом вокруг, все притягивается к ее гравитационному притяжению, а это означает, что яблоки падают на землю, а не притягиваются к голове человека.
Расстояние также влияет на гравитацию. Если объект находится далеко, то гравитационное притяжение слабее. Например, в космосе есть точка, где притяжение Марса становится сильнее притяжения Земли.
Фундаментальные силы во Вселенной

По мнению физиков, четыре фундаментальные силы Вселенной — это гравитация, электромагнитные, слабые и сильные взаимодействия. Силы изменяют движение объекта, и эти четыре фундаментальные силы определяют, как все во Вселенной взаимодействует. Гравитация — самая слабая сила, но она наиболее легко видима и оказывает наибольшее влияние на крупномасштабном уровне. Это не только причина, по которой люди могут ходить по Земле, но и удерживает планеты, вращающиеся по орбите вокруг Солнца, и Солнце на своем месте в галактике.
Древняя история гравитационной теории

Древние греки верили, что сила, притягивающая предметы к Земле, была внутренней тяжестью, а не внешней силой. Тяжелые люди естественным образом притягиваются к Земле, в то время как легкие языки пламени прыгают к небу. Напротив, индийские ученые, в частности Арьябхата, говорили, что некая сила удерживает объекты на Земле, хотя его теория помещает Землю в центр вселенной. В 600-х годах н. э. математик Брахмагупта был первым, кто описал гравитацию как силу притяжения.
Гравитационная теория эпохи Возрождения

Говорят, что Галилей бросал предметы со стороны падающей Пизанской башни, чтобы наблюдать, что происходит, когда они падают. Независимо от того, была ли задействована башня или нет, Галилей обнаружил, что все объекты имеют тенденцию ускоряться с одинаковой скоростью при падении. Другие ученые основывались на своей работе, а Гримальди и Риччоли вычислили гравитационную постоянную. Другие работы по гравитации сосредоточены вокруг астрономии и Иоганна Кеплера, построенного на этих теориях для расчета орбит известных планет.
Закон всемирного тяготения

Другая легенда о гравитации гласит, что Исаак Ньютон был поражен падающим яблоком и понял, что должна быть сила, заставляющая вещи падать на землю. Он написал уравнение, в котором описывается сила гравитации, показывающее, что чем массивнее объекты, тем больше сила притяжения между ними. Оно также показало, что чем дальше они находятся, тем слабее тяга. Некоторые планеты двигались так, что не могли объяснить это уравнение, но по большей части оно существовало веками.
Эйнштейн и общая теория относительности

Теория общей относительности Эйнштейна изменила взгляд физиков на гравитацию. Считается, что воздействие гравитации вызвано не силой, а кривой в пространстве-времени, которая возникает вокруг крупных объектов, а скорее похожа на шар для боулинга, сидящий на батуте. Эта теория объяснила странную орбиту Меркурия и установила ньютоновскую гравитацию на его голову, поскольку гравитация больше не была силой, а следствием геометрии.
Что делает гравитация?

Гравитация оказывает несколько воздействий на реальный мир. Помимо того, что гравитация не только удерживает предметы на земле, но и придает им вес. Объекты меньше весят на планетах с меньшей гравитационной тягой. Гравитация Луны — это сила, которая создает океанские приливы. Гравитация также удерживает Землю на комфортном расстоянии от Солнца и удерживает атмосферу на месте, давая всем живым существам воздух, пригодный для дыхания, и защищая их от солнечного излучения.
Гравитация и сотворение Вселенной.

Гравитация также является существенным элементом в создании Вселенной. Газы, существующие во Вселенной, притягиваются друг к другу под действием гравитации и объединяются в крупные объекты, в том числе звезды и планеты. Некоторые исследователи считают, что именно гравитация стабилизировала частицы после Большого взрыва, остановив коллапс Вселенной. Гравитация притягивает солнечные системы друг к другу, образуя галактики, и как таковая является основополагающим элементом в создании Вселенной.
Гравитация и научные исследования

Научные исследования в области гравитации будут продолжаться и в будущем. Теория относительности объясняет некоторые аномалии в ньютоновской гравитации; во Вселенной все еще есть тайны, которые ученые не могут объяснить. Гравитация не вписывается в теорию квантовых полей, и ученые до сих пор исследуют, как она соединяется с другими фундаментальными силами. Исследования гравитации также имеют более практическое применение. Космические аппараты НАСА отслеживают изменения гравитации Земли, что помогает ученым отслеживать изменения уровня моря и земной коры.
Что такое гравитация: короткий и понятный ответ
Гравитация — это сила, которая действует на каждого обитателя Земли, впрочем, как и на саму Землю. Утрируя, можно сказать, текущий вид Вселенной существует благодаря силе притяжения. А значит пора разобраться, что такое гравитация простыми словами.
Определение гравитации
Слово «гравитация» происходит от латинского gravitas — вес.
Гравитация — сила, с помощью которой планета или другое тело притягивает объекты к своему центру. Именно благодаря ей мы не улетаем в космос, всегда притягиваясь к Земле. Так и планеты Солнечной системы всегда испытывают притяжение звезды и остаются на своих местах.
Как работает гравитация
Сила притяжения зависит от массы объектов и расстояния межу ними. Все, что имеет массу, имеет и гравитацию. Объекты с большей массой имеют большую гравитацию. Она ослабевает с расстоянием, и чем ближе объекты друг к другу, тем сильнее их тяготение.
Исаак Ньютон был первым, кто математически описал гравитацию и то, что она одинаково действует на все объекты во Вселенной: от падающего яблока до планет, которые движутся вокруг звезды. Так и появился закон всемирного тяготения, которого придерживались веками.
Сила притяжения F между двумя материальными точками с массами и , разделёнными расстоянием , действует вдоль соединяющей их прямой, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния.
Здесь — гравитационная постоянная, равная 6,67408(31)·10−11 м³/(кг·с²).
Кстати, падение яблока на голову Ньютона — это миф. Он действительно любил отдыхать под яблоней, и наблюдения за падающими яблоками натолкнуло его на мысль о всемирном тяготении. Но по голове Ньютона ничего не било.
Теория Ньютона объясняла гравитацию как некую силу. Но в последствии появилась теория Эйнштейна, в основе которой подход геометрический. Если простыми словами: крупные объекты искривляют пространство-время вокруг себя, а в это «искривление» попадают другие объекты.
Визуализация гравитации. Альберт Эйнштейн описал гравитацию как кривую в пространстве, которая охватывает такой объект, как звезда или планета. Анимация: NASA
Этот принцип хорошо показан в этом ролике:
Теория Энштейна — является действующей на сегодня.
Но не идеальной…
Рекомендуем: Что такое чёрная дыра
Насколько важна гравитация?
Очень важна! Гравитация — это одна из сил фундаментальных взаимодействий, которым подчиняется всё, что есть во Вселенной. Вот эти взаимодействия:
- гравитационное;
- электромагнитное;
- сильное;
- слабое.
Именно благодаря им мир такой, каким мы его знаем. Гравитация в этом списке является самым крупномасштабным, но одновременно и самым слабым взаимодействием, остальные — определяют взаимодействия на уровне частиц.
Ещё много интересного в наших соцсетях
Как гравитация повлияла на Вселенную
Именно сила притяжение создает звезды и планеты, собирая вместе материал, из которого они сделаны. Гравитация — это то, что удерживает планеты на орбите вокруг Солнца и то, что удерживает Луну на орбите вокруг Земли.
Это интересно: Почему спутники не падают
Роль гравитации для землян
Те условия, в которых мы живём, были бы невозможны без неё. Она удерживает нашу планету на одинаковом расстоянии от Солнца, не позволяет атмосфере покинуть пределы Земли, как и всему, что находится на её поверхности. Гравитационное притяжение Луны притягивает к себе моря, вызывая приливы океана.
Луна и приливы на Земле
Гравитация очень важна для нас. Мы не могли бы жить на Земле без неё. Тяготение Солнца удерживает Землю на орбите вокруг него на постоянном комфортном для жизни расстоянии. Сила притяжения удерживает нашу атмосферу и воздух, которым мы дышим.
Гравитация — это то, что скрепляет наш мир.
Однако гравитация не везде одинакова на Земле. Она немного сильнее в местах с большей массой под землей, чем в местах с меньшей массой.
Есть ли гравитация у человека?
У каждого материального объекта есть своя сила притяжения, и человек не является исключением.
Гравитация и движение планет в Солнечной системе.
Всем нам известно строение Солнечной системы еще из школьных уроков по астрономии. Также нам дано некое представление о происхождении планет и даже объяснили их движение с помощью некоторых законов физики, которые нам преподносят, как истинные. Однако у многих уже зародились сомнения в истинности этих теорий и по-прежнему остаются вопросы: как же все-таки появились планеты в Солнечной системе и откуда взялась планета Земля?
Давайте попробуем на основе уже имеющихся данных разобраться без формул и серьезных расчетов в движении планет в Солнечной системе. Так же попробуем разобраться в зарождении самих планет и выяснить, что же такое — гравитация. Сразу оговорюсь: данный анализ происходящих процессов сильно упрощен и отличается от официальных постулатов, хотя нисколько им не противоречит.

Эти фотографии нам дают понять, что существуют одинаковые принципы движения материи на Земле и в космосе. В основе этого движения — вихревое вращение, закручивающее потоки в виде спирали. Если с водоворотом и торнадо все понятно, то что же вращается в галактике? Правильно, эфир.
Что же такое эфир?
Об эфире догадывались еще древнегреческие философы. У Платона эфир выступает как особая, небесная стихия, четко отграниченная от четырех земных – земли, воды, воздуха и огня. Аристотель наделял эфир способностью к вечному круговому (самому совершенному) движению и трактовал его как перводвигатель, имманентный мирозданию. Лукреций также рассматривал эфир как начало, двигающее небесные тела и состоящее из самых легких и подвижных атомов.
Физики нового времени полагают, что эфир заполняет собой все пространство и состоит из мельчайших частиц размером в миллионы раз меньше электрона, что позволяет им беспрепятственно пронизывать насквозь все материальные тела. Именно эфир является основой магнитного поля, а также выступает средой для движения света и других электромагнитных волн.
Взяв в руки два магнита и приблизив их друг к другу одноименными полюсами, можно почувствовать поток этого эфира. Чем ближе магниты, тем труднее их соединить, а следовательно, тем плотнее поток эфира. Какова форма этого потока, мы могли видеть еще в школьных учебниках физики, где наглядно изображали направление магнитных линий, проводя опыт с металлическими опилками и постоянным магнитом.

Здесь мы и видим форму магнитного поля — эфирного потока. Таким образом формой магнитного поля в постоянном магните является тороид. Модель эфирного потока в виде тороида выглядит так:

Точно такой же эфирный вихрь и вращает звезды в галактике, которые под действием центробежных сил растянулись по горизонтальной плоскости в центральной части тороида. Аналогично движутся потоки воды в водовороте и воздушные потоки в торнадо, хотя обычно они имеют неправильную вытянутую форму, хоботом опускаясь к земле или ко дну.
Солнечная система.
Давайте рассмотрим Солнечную Систему.
Для начала рассчитаем расстояния между орбитами в астрономических единицах:

Здесь мы видим, что внешние орбиты равноудалены друг от друга, а внутренние постепенно уплотняются к центру. Причем, глядя на числа, создается впечатление, что на месте пояса астероидов должна быть еще одна планета. И планета эта существует! Один из самых крупных астероидов — Церера назван малой планетой. И все это благодаря его шарообразной форме.
Далее для удобства воспользуемся известной флешкой:
Наведем курсор мышки на календарную шкалу и нажав левую кнопку, покрутим планеты в одну и в другую сторону.
Посмотрите, чем ближе планеты к центру системы, тем быстрее они вращаются. Та же схема работает и на примере планетарной системы с ее спутниками. Все это напоминает водоворот. Движение планет аналогично движению звезд в галактической спирали. Очевидно, что вокруг Солнца вращается огромный эфирный вихрь, на орбитах которого вращаются вихри поменьше — планеты, которые, в свою очередь, также на орбитах имеют малые вихри — спутники. Так может быть этот эфирный вихрь и рождает гравитацию? И что же первично? Планета или ее гравитация? Скорее всего гравитация. Именно этим и обусловлена шарообразная форма планеты с самого начала ее зарождения. Получается, что для зарождения звезды или планеты сначала должен родится эфирный гравитационный вихрь. Назовем его просто гравитационный вихрь (ГВ).
Совершенно очевидно, что пояс астероидов — это существовавшая в прошлом планета. Ей даже придумали название — Фаэтон. И, судя по всему, Фаэтон был разрушен каким то очень крупным объектом. А если планета и была разрушена, то это не означает разрушение самого ГВ. Что мы и наблюдаем на примере карликовой планеты Церера, которая остается на месте прежде существовавшей планеты Фаэтон. Его шарообразная форма — первый признак наличия гравитации.
Как все происходит? Проведем аналогии с торнадо. Торнадо образуется при столкновении больших воздушных масс. Видимо гравитационный вихрь рождается аналогичным образом: при столкновении солнечного ГВ с вихрем другой звезды или какого-либо другого объекта со значительной гравитацией, закручивается планетарный ГВ. И происходит это на краю Солнечной системы.
Что же находится в центре такого новоиспеченного ГВ? В центре образуется область с пониженным давлением, куда начинает стягиваться пространство. И как же эта область называется? Правильно! Название этому уже есть — черная дыра (ЧД). Вновь созданная ЧД начинает втягивать в свой центр материю до тех пор, пока не восполнит свою гравитационную массу и не покроется твердой оболочкой, вокруг которой будет сформировано облако газа и пыли. Так рождается планета. Таким образом новоиспеченная планета выглядит как газопылевое облако шарообразной формы.
А теперь взгляните на наши планеты: Меркурий, Венера, Земля, Марс — планеты с твердой поверхностью, Юпитер, — жидкая поверхность, Сатурн, Уран, Нептун и Плутон — с газообразной поверхностью, разумеется, внутри все они твердые. Что же мы видим? Налицо эволюция планет от периферии к центру. Что опять подтверждает теорию движения по спирали к центру Солнечной системы. Таким образом, зарождаясь на краю Солнечной системы, планеты постепенно приближаются к Солнцу и в конечном итоге, умирая, падают на него. Вероятно на минимальном расстоянии от Солнца планета, нагреваясь, вспыхивает как вторая маленькая звезда. Может быть именно это явление и видится нам как двойная звездная система?
В момент зарождения планетарных вихрей, возможно зарождаются и малые вихри на орбитах — будущие спутники. Движение спутников в каждой планетарной системе происходит по тем же законам — от периферии к центру. Спутники планет, двигаясь по спирали, со временем падают на планету, как и планеты на Солнце. Взгляните на фотографию Марса:

Это так называемый Большой каньон или Долина Маринер. Считается, что это след от соприкосновения с крупным астероидом. Однако совершенно ясно видно, что этот след тянется по закруглению планеты почти на четверть окружности. Значит удар был не по касательной, как мог быть от астероида или кометы, а от объекта находящегося на орбите Марса. Большой каньон это не что иное, как след от падения спутника Марса!
Сатурн имеет 7 крупных шарообразных спутников, Юпитер имеет 4 крупных спутника, Марс имеет два спутника и след от падения третьего, Земля имеет один спутник, Венера и Меркурий, как самые старые планеты — ни одного. Что опять же указывает на эволюцию планет от периферии к центру Солнечной системы.
Какие напрашиваются выводы? А выводы напрашиваются такие:
Гравитация не рождается массой тела, наоборот — сначала появляется гравитация, а потом в этом месте растет крупное космическое тело. Собственную гравитацию имеют планеты, их спутники, звезды, центры галактик и черные дыры. Другие космические объекты — астероиды, кометы, метеориты — не имеют собственной гравитации. Первичными признаки собственной гравитации являются: шарообразная форма, вращение вокруг собственной оси и движение по орбите.
Полезные ссылки:
Причуды гравитации в Солнечной системе
Интересный материал по теме.
Одна звезда, восемь планет, пояс астероидов — основные объекты Солнечной системы знакомы нам с детства. Однако в ней есть и другие, более загадочные небесные тела и области, возникшие под воздействием гравитации Солнца и планет, и они остаются неизвестными для большинства из нас. «Теории и практики» выбрали шесть необычных явлений, порожденных силой тяготения.
Точки Лагранжа
Так называемые точки Лагранжа есть в любой системе небесных тел. Это пять гравитационных ловушек, которые возникают на орбите, когда объект поменьше (например, спутник) вращается вокруг объекта побольше (например, планеты). Притяжение двух тел в этом случае так велико, что в точках Лагранжа оно нейтрализует действие всех остальных сил. В результате третий, совсем маленький объект — скажем, астероид — не может выйти из гравитационной ловушки и начинает вращаться вокруг планеты вместе с ее спутником. Они двигаются по одной орбите, как братья-близнецы, причем несчастный астероид не может ни врезаться в спутник, ни улететь прочь.
В системе Солнце — Юпитер «пленниками» точек Лагранжа L4 и L5 стали сразу две группы астероидов: «троянцы» и «греки», названные в честь персонажей «Илиады» Гомера. Они застряли на орбите Юпитера, под углом в 60° к нему, и с тех пор не могут за ним угнаться.
Щель Кассини
Темный промежуток между кольцами Сатурна, который сегодня можно увидеть даже в любительский телескоп, носит загадочное название «щель Кассини». Ее ширина составляет 4,537 км: как расстояние между Москвой и Мадридом.
Долгие годы астрономы считали, что щель Кассини пуста. Однако благодаря полетам «Вояджера» выяснилось, что это совсем не так. Этот промежуток наполнен частицами льда и силикатной пыли, из которых состоят кольца планеты. Однако плотность потока частиц здесь снижена из–за сильного орбитального резонанса колец (соотношения периода их обращения), а также из–за притяжения «спутника-пастуха» Сатурна, Мимаса, который помогает ему удерживать кольца на месте. По плотности щель Кассини можно сравнить с кольцом С — вторым по удаленности от Сатурна.
Щели Кирквуда
Щели, или люки Кирквуда — это пустоты, которые образуются в поясе астероидов из–за чудовищной гравитации другого водородного гиганта — Юпитера. Притяжение этой планеты сбивает астероиды с прежней траектории. В результате создается впечатление, что они стараются избегать мест, где грозная планета способна захватить их в плен. Углеродные, силикатные и металлические глыбы исчезают из одних мест и «толпятся» в других.
В местах наибольших скоплений астероиды сталкиваются друг с другом, разбиваются на куски, лишаются своих лун или приобретают их. Многие из них покидают пояс: улетают прочь или устремляются к Солнцу.
Пояс Койпера
Астероиды в Солнечной системе можно встретить не только между орбитами Марса и Юпитера или возле планет — в качестве спутников. За орбитой Нептуна — восьмой и последней «солнечной» планеты — располагается так называемый пояс Койпера. Он похож на знакомый нам пояс астероидов, однако по ширине превосходит его в 20 раз, а по объему, по некоторым оценкам, — в 200 раз. По форме пояс Койпера напоминает гигантский бублик. Он наполнен материалом, оставшимся после формирования Солнечной системы: астероидами и карликовыми планетами, к которым с 2006 года был причислен и Плутон.
В отличие от малых тел пояса астероидов, объекты пояса Койпера, в основном, состоят не из металлов и горных пород, а из метанового, азотного и водяного льда. Иначе говоря, по составу они напоминают кометы. Раньше считалось, что именно пояс Койпера служит источником короткопериодичных комет (таких, как комета Галлея), которые возвращаются к Солнцу чаще, чем раз в 200 лет. Однако сегодня нам известно, что настоящие источники комет располагаются дальше.
Рассеянный диск
В действительности источником комет с коротким периодом обращения служит так называемый рассеянный диск. Это область настоящего хаоса, лежащая на окраине Солнечной системы. Он заселен ледяными малыми телами, которые лишены возможности встать на устойчивую орбиту из–за своей удаленности от звезды и крупных планет. Их движение нестабильно, они блуждают в пространстве без яркого света и устойчивой гравитации, во тьме и беспорядке. Нередко объекты рассеянного диска просто выкидывает за его пределы и даже за пределы Солнечной системы.
Один из главных «резидентов» рассеянного диска — карликовая планета Эрида, названная в честь греческой богини раздора. Ее огромная орбита поражает воображение. Солнечный свет идет до Эриды больше 13 часов. Температура на поверхности планеты составляет от −253 до −230 °C. Эрида покрыта метановым снегом, а также азотным, этановым и этиленовым льдом, поэтому в небе, при взгляде через телескоп, она светится очень ярко.
Существует предположение, что раз в 250 лет, при максимальном приближении к Солнцу, замерзшие газы на поверхности планеты оттаивают, и у Эриды появляется атмосфера. По прогнозам, в следующий раз это может произойти в середине XXIII века — в 2250 году.
Облако Оорта
Облако Оорта — последняя область, где Солнце оказывает заметное влияние на движение космических объектов. Правда, пока ее существование не удалось подтвердить напрямую, и мы опираемся лишь на косвенные доказательства.
Считается, что облако является остатком исходного протопланетного диска, из которого позже сформировалось Солнце и небесные тела вокруг него. Оно расположено на гравитационной границе Солнечной системы и напоминает огромный двухслойный пузырь, наполненный одинокими кометами и холодными планетозималями — нерожденными планетами. Внутренняя часть облака имеет форму диска, внешняя напоминает шар и подчиняется не только солнечной гравитации, но и притяжению соседних звезд, а также самой Галактики.
Небесные тела облака Оорта, в основном, состоят из замерзшего угарного газа, синильной кислоты, метана, этана и воды, а также из скалистых пород. В отличие от комет из рассеянного диска, период обращения кометных тел из облака Оорта огромен и может составлять тысячи лет. К примеру, потрясающе яркая комета Хейла-Боппа, которую в 1996 и 1997 годах можно было невооруженным глазом увидеть с Земли, по прогнозам, вернется к центральной части Солнечной системы лишь в 4390 году.
Кандидатом в объекты облака Оорта является также карликовая планета Седна, получившая имя в честь эскимосской богини морских животных. Это самое далекое небесное тело нашей родной системы из всех, что на сегодняшний день нам удалось открыть. Кроме того, Седна имеет самый длинный период обращения вокруг Солнца: порядка 11,5 тысяч лет. Карликовая планета окрашена в интенсивный красный цвет и покрыта смесью метанового, водяного и азотного льда с примесью толинов — смеси органических сополимеров, которые, вероятно, были химическими предшественниками жизни на Земле. Ряд исследований указывает на то, что на Седне есть подземный водяной океан, который поддерживает в жидком состоянии процесс радиоактивного распада в недрах планеты.
Источник.
Но почему? Что происходит?
Хотя мы только начали понимать, что это такое, этот феномен размышлял тысячелетиями.
Например, когда-то греческие философы считали, что планеты и звезды являются частью царства богов. По их оценке, они были подвержены так называемому «естественному движению».
Пока они не разработали концепцию намного дальше этого, она останется доминирующей идеей в западной мысли до работы Галилея и Браге в 16-м веке.
Их работа поможет вызвать революцию в нашем понимании гравитации, которая в конечном итоге приведет к Исааку Ньютону.
Гравитация, как утверждал Ньютон, — это сила, которая удерживает Землю на орбите вокруг Солнца. Как вы помните из школьных дней, гравитация обычно определяется как:
«Сила, с помощью которой планета или другое тело притягивает объекты к своему центру. Сила гравитации удерживает все планеты на орбите вокруг Солнца». — НАСА.
Другими словами, что-либо с массой оказывает силу на любую другую вещь с массой и оказывает на нее воздействие.Чем больше масса объектов и чем меньше расстояние между ними, тем сильнее сила притяжения, которое они оказывают друг на друга.
Всякий раз, когда вы подпрыгиваете в воздухе, случайно выбиваете что-то со стола или бросаете мяч в парке, чтобы ваша собака могла поймать, вы интуитивно знаете последствия своих действий. Все они, в конце концов, возвращаются на землю.
Эйнштейн позже предложил бы совершенно другое объяснение гравитации, чем Ньютон.«Это говорит о том, что гравитационные и инерционные силы имеют сходную природу и часто неразличимы.
Чтобы проиллюстрировать это, представьте, что вы находились на ракетном корабле без окон и не могли видеть внешнюю вселенную из своего окружения. В этом случае было бы невозможно определить, является ли сила вниз, которую вы ощущаете как гравитация, реальной силой или следствием ускорения ракеты в определенном направлении.
Мы понимаем гравитацию?
Поставь просто, да и тоже нет. Хотя это одно из наиболее широко изучаемых явлений природы во вселенной, мы до сих пор не понимаем этого.
Это одна из самых больших проблем в физике сегодня. Многие физики надеются когда-нибудь создать единую теорию макро- и квантовой физики, которая поможет объяснить, что происходит.
Как нам помогает гравитация?
Гравитация — одна из самых фундаментальных «сил» во вселенной. Аргументы о том, как это работает в стороне, какой бы ни была гравитация, это очень важный элемент для жизни на нашей планете.
Гравитация — причина, по которой объекты на Земле имеют вес и не просто уплывают в космос.Если бы вы жили на планете с меньшей массой, вы бы весили меньше и смогли бы прыгнуть намного выше.
Гравитация также удерживает Землю в так называемой «Зоне Златовласки» — расстоянии от нашего Солнца, где вода может существовать в жидкой форме. Это просто так жизненно важно для жизни.
Gravity также помогает сохранять атмосферу Земли, обеспечивая нам воздух для дыхания. Например, Марс составляет менее половины размера Земли и составляет около одной десятой массы Земли. Меньшая масса означает меньшее гравитационное притяжение, и на самом деле атмосфера Марса имеет плотность примерно 1/100000000, как у Земли.
Гравитация также играет важную роль в поддержании нашей планеты вместе. Гравитация также удерживает луну на орбите вокруг Земли. Гравитационное притяжение луны притягивает к себе моря, вызывая приливы океана.
Но интересно, что сила притяжения не одинакова во всех местах на Земле. Он немного сильнее в местах с гораздо большей массой под землей, чем в местах с меньшей массой.
Мы знаем это из-за двух космических кораблей НАСА и их миссии по гравитационному восстановлению и климатическому эксперименту (GRACE).
Что необходимо, чтобы обеспечить средство ускорения в одном направлении, которое, согласно Эйнштейну, должно производить эффект, подобный гравитации. Это может быть сделано с помощью линейного ускорения, такого как ракета, или посредством углового момента, то есть центростремительного эффекта или ускорения.
Это общая тема во многих научно-фантастических книгах и фильмах. Подумайте о вращающемся космическом корабле в «2001: Космическая одиссея», например.
По мере того, как корабль достаточно велик, он должен иметь возможность создавать на своих обитателей силу, которая была бы почти неотличима от гравитации на Земле.
interestingengineering.com
