Матрикс состав: Краска для волос Матрикс в интернет магазине Kosmetika-proff.ru

Matrix 5.0 2,27 кг от Syntrax

Отличительные особенности Syntrax Matrix

Технологи компании Syntrax при создании протеинового комплекса Matrix® полностью отказались от таких дешевых источников белка как денатурированные казеинаты кальция и натрия.

В состав Matrix® входят только протеины высочайшего качества: ультрафильтрованный сывороточный протеин, ультрафильтрованный молочный протеин, натуральный яичный альбумин и пептиды глютамина. Они стоят намного дороже, но качество является залогом эффективности данного продукта.

Matrix® не только обладает превосходным вкусом, но и положительно влияет на состояние здоровья.

Все источники белка имеют по отдельности свои сильные и слабые стороны. Например, яичный протеин идеально усваивается и содержит большое количество факторов роста, но при этом очень недешев.  Сывороточный протеин быстрее всего усваивается и улучшает иммунитет. Казеин долго усваивается и поэтому способен подпитывать мышцы аминокислотами длительный промежуток времени.

Соответственно, хотя каждый из источников белка имеет много преимуществ, но их комплекс будет работать лучше, сочетая в себе все их плюсы и минимизируя недостатки.

Благодаря сочетанию высококачественных источников белка Matrix® обладает одним из лучших аминокислотных профилей на рынке спортивного питания. Он способствует увеличению мышечной массы и уменьшению жировой, обладает антиоксидантным действием, улучшает состояние иммунной системы, не оказывает негативного воздействия на почки и многое др.

Так как в  состав Matrix® входят протеины с различной скоростью усвоения, его можно принимать в любое время: как после тренировки, так и перед сном.

Несмотря на высочайшее качество стоимость Matrix® 5.0 относительно невелика, благодаря использованию экономичной ламинированной упаковки, которая позволяет сохранить все качества продукта, не увеличивая его цену.

Применение Matrix® 5.0:

Разведите 1 мерную ложку продукта (32 грамма) в 200-300 мл воды, обезжиренного молока или сока по вашему вкусу. Принимайте в течение дня между приемами пищи. Общее количество порций  зависит от массы тела, интенсивности  тренировок, общего потребления белковой пищи и калорийности рациона. Общее дневное потребление белка для ведущих активный образ жизни людей,  рекомендуется от 1,5-2 грамм на 1 кг массы тела.

Ингредиенты: белковый комплекс (концентрат сывороточного белка, концентрат молочного белка (ультрафильтрованный и неденатурированный; включая мицеллярный казеин), яичный альбумин (неденатурированный), гидролизованный пшеничный глютен (содержит пептиды глютамина)), какао, натуральный и искуственный ароматизаторы, соевый лецитин, хлорид натрия, ацесульфам К, сукралоза.

*Рекомендованная суточная норма указана исходя из калорийности рациона – 2000 ккал. Калорийность может быть увеличена или уменьшена в соответствии с потребностями.

Краска для волос Matrix (Матрикс): палитра, особенности и разновидности

Красивая прическа – это залог привлекательности, но она требует существенных затрат времени и сил, кроме того, очень важно подобрать правильные косметические средства. Профессиональная краска для волос Matrix сегодня пользуется спросом не только среди стилистов, но и обычных женщин. Широкой популярности способствует не только высокое качество продукции бренда и огромный выбор цветов, но также безопасность и мягкое воздействие.

Появилась профессиональная краска для волос Матрикс благодаря американскому парикмахеру Анри Миллеру в 1980 году. Решение создать собственный бренд появилось из-за недостатка действительно качественных средств для реализации идей стилистов. Логическим продолжением этой линии для Анри стало также создание команды профессионалов в области парикмахерского искусства, которые наглядно демонстрируют, почему надо купить краску Matrix. Подобный подход позволил Миллеру занять почетное место на рынке средств для стайлинга, окрашивания и ухода за локонами. По данным компании, краску для волос Matrix купить можно более чем в пятидесяти странах мира, а специальные средства используются примерно в четверти миллиона салонов.

Краска Matrix Socolor Beauty

Средства для окрашивания волос сегодня очень популярны, поскольку с их помощью можно кардинально изменить имидж, но и далеко не все они дают ожидаемый результат. По этой причине стойкая крем-краска Matrix так востребована. Она обеспечивает глубокое окрашивание, а также придает обворожительный блеск.

Палитра краски для волос Матрикс Соколор включает в себя несколько десятков оттенков, в том числе и специальный бесцветный Clear, который нужен для модного пастельного окрашивания. Такой ассортимент позволяет подобрать оптимальный вариант на любой вкус: от мягких блондов до насыщенных каштановых и ярких красных тонов.

Выгодным преимуществом краски Матрикс Соколор является включение в состав специального комплекса Cera-Oil, который защищает и восстанавливает структуру волос. Не секрет, что во время покраски любым средством, даже самым бережным и щадящим, нарушается поверхностный слой. Такие нарушения структуры делают расчесывание болезненным, а также приводят к ломкости и сухости. Cera-Oil же надежно защищает локоны и восстанавливает мельчайшие повреждения.

Крем-краска Matrix Color Sync

Для того, чтобы окрашенные волосы долго сохраняли насыщенный оттенок и красивый блеск, не обязательно регулярно использовать стойкие средства. Содержащиеся в их составе компоненты при частом применении могут нанести существенный вред, привести к сухости и даже выпадению. Гораздо лучше воспользоваться тонирующей краской для волос Matrix Color Sync без аммиака, палитра которой включает множество оригинальных цветов. Она отлично ложится, делает оттенки ярче или насыщеннее, в зависимости от концентрации пигмента, что позволяет безопасно экспериментировать.

Краска Матрикс без аммиака также имеет еще одно интересное свойство: улучшать структуру волос, поскольку в состав входит особый керамидный комплекс. Он выравнивает поверхность, устраняя пористость и разглаживая микроскопические чешуйки. За счет этого существенно улучшается внешний вид, расчесывание и укладка становятся простыми и приятными. При помощи краски Матрикс Колор Синк можно реализовать самые оригинальные идеи, за что ее очень любят стилисты. Она идеально подходит для тонирования и мелирования. Интересными также являются необычные цветовые решения, такие как пастельные оттенки и металлик. Первые сегодня пользуются очень большим спросом, можно сказать, находятся на пике моды. Подобного эффекта можно также добиться с любым цветом палитры красок Матрикс за счет специального прозрачного крем-геля. Он как бы разбавляет состав, делая конечный результат на светлее. Металлики же придают невероятно яркий блеск, достичь которого можно только при помощи лаков с металлическими частицами, наносящими серьезный вред.

Краска Matrix для седых волос

И для женщин, и для мужчин седина – это серьезная проблема, которая способна испортить любой образ. Даже нескольких волосков в прическе достаточно, чтобы перечеркнуть результаты длительной процедуры укладки. Стоит справедливо отметить, что некоторым она идет, но только в тех случаях, когда проявляется равномерно. В остальных случаях на помощь приходит краска для седых волос Матрикс.

Выбрать правильный вариант довольно просто: и стойкая, и безаммиачная линии гарантируют закрашивание до пятидесяти процентов седины. В иных случаях стоит купить краску Матрикс для седых волос. Специально разработанная формула позволяет получить яркий равномерный цвет по всей длине.

Выбирая, какую краску Матрикс купить для решения проблемы седины, стоит оценивать ее масштабы. В тех случаях, когда серебристых прядей менее семидесяти процентов, а подвергать локоны воздействию стойких средств нежелательно, можно отдать предпочтение специальной линии Color Sync Extra Coverage. Она включает в себя шесть естественных оттенков, а также специальный комплекс растительных масел и керамидов, улучшающих структуру и устраняющих пористость. За счет этого, окрашивание превращается в полноценный уход за волосами.

Если седины больше, стоит обратить внимание на палитру цветов краски Matrix Socolor Beauty Dream Age. Она включает в себя шестнадцать естественных оттенков: от теплого золотистого блонда до насыщенного красно-коричневого. Особенностью этой линейки является специальный комплекс пигментов, которые придают многогранный мультирефлекторный блеск. За счет него оттенок выглядит максимально естественным: мерцающие полутона не вызовут даже мысли о том, что Ваши волосы окрашены. Кроме того, в красители входит особый ухаживающий комплекс с натуральными маслами Cera-Density. Он существенно снижает воздействие окислителей, а также исправляет структуру, придает гибкость, эластичность и жизненную силу.

Другая продукция Matrix

Одними красками и проявителями цвета Матрикс не ограничивается. Компания производит также широкий спектр товаров для стилистов, в частности, уникальные средства для стайлинга. Серия Vavoom позволяет реализовать самые смелые идеи, поскольку особый состав обеспечивает надежную и долговременную укладку, но не отягощает волосы. Невероятный объем не нарушает структуру прядей, а потому уложенные в прическу волосы выглядят еще более здоровыми и естественными, будто их никогда не касалась рука парикмахера.

Компания также выпускает высококачественные и эффективные средства для ухода. Особое место среди них занимает линейка BIOLAGE, которая используется для профессионального ухода и восстановления. В состав продуктов из этой серии входят природные комплексы керамидов, которые укрепляют и разглаживают поверхность каждого волоска, а также уникальные растительные экстракты, насыщающие витаминами и питательными веществами. Они идеально подходят для восстановления после экспериментов с окрашиванием и экстремальной укладкой, при которой применялись высокие температуры.

А линейка Total Results отлично подходит для применения в домашних условиях. Она включает в себя основные направления для решения наиболее распространенных проблем с волосами. Термозащитные бальзамы и шампуни образуют особую мембрану, которая надежно защищает при укладке с нагревом более двухсот градусов. Кроме того, они питают и отталкивают грязь. Средства для дополнительного объема создают эффект профессиональной укладки.

Восстанавливающая серия помогает решить проблему истонченных и поврежденных волос в домашних условиях. Она включает в себя как средства для ежедневного применения, так и маску для интенсивного ухода. А разглаживающие шампуни, масла и бальзамы позволяют исправить структуру, сделав расчесывание легким и приятным. В линейку также входят средства для окрашенных и седых волос, которые изготавливаются с учетом особенных требований.

Как и большинство товаров для профессиональных стилистов, продукция этого бренда не встречается на полках обычных магазинов и специализированных отделов супермаркетов. Но это не помешало миллионам покупателей оценить преимущества высококачественной американской косметики для волос, поскольку можно приобрести ухаживающие средства, расходные материалы и краску Матрикс в нашем интернет-магазине по доступным ценам.

У нас представлен широкий ассортимент продукции бренда Matrix, потому по выгодной цене можно приобрести купить не только краску, но и другие средства для волос. При этом, все товары гарантированно являются оригинальной косметикой, произведенной с учетом высоких стандартов качества.

Умножение матриц

Цели

1. Понимать композиции преобразований.
2. Понимать взаимосвязь между матричными произведениями и композициями матричных преобразований.
3. Освойте базовую алгебру с матрицами.
4. Рецепт: умножение матриц (два способа).
5. Рисунок: композиция трансформаций.
6. Словарное слово: состав .

В этом разделе мы изучаем композиции преобразований. Как мы увидим, композиция — это способ объединения трансформаций в цепочку. Композиция матричных преобразований соответствует понятию умножения двух матриц вместе. Мы также обсуждаем сложение и скалярное умножение преобразований и матриц.

Композиция в линейной алгебре означает то же самое, что и в исчислении. Вот определение.

Определение

Пусть T:Rn→Rm и U:Rp→Rn — преобразования. Их композиция представляет собой преобразование T◦U:Rp→Rm, определяемое

(Т◦U)(х)=Т(U(х)).

Составление двух преобразований означает объединение их в цепочку: T◦U — это преобразование, которое сначала применяет U, а затем применяет T (обратите внимание на порядок операций). Точнее, чтобы оценить T◦U на входном векторе x, сначала вы оцениваете U(x), затем берете этот выходной вектор U и используете его в качестве входного вектора T: то есть (T◦U)(x )=Т(U(x)). Конечно, это имеет смысл только тогда, когда выходы U являются действительными входами T, то есть когда диапазон U содержится в домене T.

RpxRnU(x)RmT◦U(x)UTT◦U

Вот изображение композиции T◦U как «машины», которая сначала запускает U, затем получает его выходные данные и передает их в T; аналогичная картина есть в этом подразделе раздела 3.1.

T◦UUTRpxRmT◦U(x)U(x)Rn

Домен и домен композиции

• Для определения T◦U кодовый домен U должен совпадать с доменом T.
• Домен T◦U является доменом U.
• Кодовый домен T◦U является кодовым доменом T.

Пример (функции одной переменной)

Интерактив: Состав матричных преобразований

Interactive: Преобразование, определенное в шагах

Interactive: Преобразование, определенное в шагах

Напомним из этого определения в Разделе 3.1, что преобразование тождества — это преобразование IdRn:Rn→Rn, определяемое IdRn(x)=x для каждого вектора x.

Окончательное свойство называется ассоциативностью . Разворачивая обе стороны, он говорит:

S◦(T◦U)(x)=S(T◦U(x))=S(T(U(x)))=S◦T(U(x))=(S◦T)◦U (Икс).

Другими словами, как S◦(T◦U), так и (S◦T)◦U являются преобразованием, определяемым сначала применением U, затем T, затем S.

Композиция преобразований , а не коммутативна вообще. То есть, вообще говоря, T◦UB=U◦T, даже когда определены обе композиции.

Пример (функции одной переменной)

Пример (Некоммутативная композиция преобразований)

В этом подразделе мы вводим, казалось бы, несвязанную операцию с матрицами, а именно матричное умножение. Как мы увидим в следующем подразделе, умножение матриц в точности соответствует композиции соответствующих линейных преобразований. Сначала нам понадобится терминология.

Обозначение

Пусть A — матрица размера m × n. Обычно мы будем писать aij для записи в i-й строке и j-м столбце. Он называется i,j записью матрицы.

a11···a1j···a1n………ai1···aij···ain………am1···amj···amnEIIIGFJJJHjthcolumnithrow

Определение (умножение матриц)

Пусть A — матрица размера m×n, а B — матрица размера n×p. Обозначим столбцы матрицы B через v1,v2,…,vp:

B=C|||v1v2···vp|||D.

Продукт AB — матрица m×p со столбцами Av1, Av2,…, Avp:

AB=C|||Av1Av2···Avp|||D.

Другими словами, умножение матриц определяется столбец за столбцом или «распределяется по столбцам B».

Пример

Для определения векторов Av1,Av2,…,Avp количество строк B должно быть равно количеству столбцов A.

Размеры матриц в матричном произведении

• Для определения AB количество строк B должно равняться количеству столбцов A.
• Произведение матрицы m×n и матрицы n×p является матрицей m×p.

Если B имеет только один столбец, то AB также имеет один столбец. Матрица с одним столбцом — это то же самое, что и вектор, поэтому определение произведения матриц обобщает определение произведения матриц на вектор из этого определения в разделе 2.3.

Если A — квадратная матрица, то мы можем умножить ее саму на себя; мы определяем его степеней как

А2=ААА3=АААи т.д.

Правило строки-столбца для умножения матриц

Напомним из этого определения в Разделе 2.3, что произведение вектора-строки и вектор-столбца есть скаляр

Aa1a2···anBEIIGx1x2…xnFJJH=a1x1+a2x2+···+anxn.

Следующая процедура нахождения матричного произведения гораздо лучше приспособлена для ручных вычислений; предыдущее определение больше подходит для доказательства теорем, таких как эта теорема ниже.

Рецепт: Правило строки-столбца для умножения матриц

Пусть A — матрица размера m×n, пусть B — матрица размера n×p, и пусть C=AB. Тогда ij-й элемент C — это i-я строка A, умноженная на j-й столбец B:

cij=ai1b1j+ai2b2j+···+ainbnj.

Вот схема:

a11···a1k···a1n………ai1···aik···ain………am1···amk···amnEIIIGFJJJHithrowb11···b1j· ··b1p………bk1···bkj···bkp………bn1···bnj···bnpEIIIIGFJJJJHjthcolumn=c11···c1j···c1p. ……..ci1···cij···cip………cm1···cmj···cmpEIIIGFJJJHijentry

Пример

Хотя умножение матриц удовлетворяет многим ожидаемым свойствам (см. конец раздела), нужно быть осторожным при выполнении матричных арифметических действий, так как есть несколько свойств, которые не выполняются в общем случае.

Меры предосторожности при умножении матриц

• Умножение матриц не является коммутативным: AB обычно не равно BA, даже если оба произведения определены и имеют одинаковый размер. См. этот пример.
• Умножение матриц не удовлетворяет закону отмены: из AB=AC не следует B=C, даже если AB=0. Например,

  К1000ЛК1234Л=К1200Л=К1000ЛК1256Л.

• Возможно при AB=0, даже если AB=0 и BB=0. Например,

  К1010ЛК0011Л=К0000Л.

Хотя умножение матриц вообще не является коммутативным, существуют примеры матриц A и B с AB=BA. Например, это всегда работает, когда A является нулевой матрицей или когда A=B. Читателю предлагается найти другие примеры.

Пример (некоммутативное умножение матриц)

Порядок действий

Цель этого подраздела — показать, что умножение матриц соответствует композиции преобразований, то есть стандартная матрица для T◦U является произведением стандартных матриц для T и для U. Это должно быть трудно поверить, что наша сложная формула для умножения матриц на самом деле означает что-то интуитивное, например, «связывание двух преобразований вместе»!

Теорема

Пусть T:Rn→Rm и U:Rp→Rn — линейные преобразования, а A и B — их стандартные матрицы соответственно, так что A — матрица размера m×n, а B — матрица размера n×p. Тогда T◦U:Rp→Rm — линейное преобразование, а его стандартная матрица — произведение AB.

Доказательство

Сначала проверим линейность T◦U. Пусть u,v — векторы в Rp. Затем

T◦U(u+v)=T(U(u+v))=T(U(u)+U(v))=T(U(u))+T(U(v))=T ◦U(u)+T◦U(v).

Если c скаляр, то

T◦U(cv)=T(U(cv))=T(cU(v))=cT(U(v))=cT◦U(v).

Поскольку T◦U удовлетворяет двум определяющим свойствам в разделе 3.3, это линейное преобразование.

Теперь, когда мы знаем, что T◦U является линейным, имеет смысл вычислить его стандартную матрицу. Пусть C — стандартная матрица T◦U, поэтому T(x)=Ax,U(x)=Bx и T◦U(x)=Cx. По этой теореме в разделе 3.3 первый столбец C — это Ce1, а первый столбец B — Be1. У нас есть

T◦U(e1)=T(U(e1))=T(Be1)=A(Be1).

По определению, первый столбец произведения AB является произведением A на первый столбец B, то есть Be1, поэтому

Ce1=T◦U(e1)=A(Be1)=(AB)e1.

Отсюда следует, что C имеет тот же первый столбец, что и AB. Тот же аргумент, примененный к i-му стандартному вектору координат ei, показывает, что C и AB имеют один и тот же i-й столбец; поскольку у них одинаковые столбцы, это одна и та же матрица.

Теорема оправдывает наш выбор определения произведения матриц. Это единственная причина, по которой матричные произведения определяются таким образом. Перефразируя:

Продукты и композиции

Матрица композиции двух линейных преобразований есть произведение матриц преобразований.

Пример (Композиция вращений)

Интерактив: Состав матричных преобразований

Interactive: Преобразование, определенное в шагах

Напомним из этого определения в разделе 3.3, что единичная матрица — это матрица размера n × n, столбцы которой являются стандартными векторами координат в Rn. Единичная матрица является стандартной матрицей преобразования идентичности: то есть x=IdRn(x)=Inx для всех векторов x в Rn. Для любого линейного преобразования T:Rn→Rm имеем

ИКм◦T=T

, и по тому же признаку мы имеем для любой m × n матрицы A мы имеем

ИмА=А.

Аналогично имеем T◦IRn=T и AIn=A.

В этом подразделе мы опишем еще две операции, которые можно выполнять над преобразованиями: сложение и скалярное умножение. Затем мы переводим эти операции на язык матриц. Это аналогично тому, что мы сделали для композиции линейных преобразований, но гораздо менее тонко.

Определение

• Пусть T,U:Rn→Rm — два преобразования. Их сумма есть преобразование T+U:Rn→Rm, определяемое формулой

  (Т+У)(х)=Т(х)+У(х).

  Обратите внимание, что добавление преобразований определяется только в том случае, если оба преобразования имеют один и тот же домен и кодовый домен.

• Пусть T:Rn→Rm — преобразование, а c — скаляр. Скалярное произведение числа c на T представляет собой преобразование cT:Rn→Rm, определяемое формулой

  (сТ)(х)=с·Т(х).

Чтобы подчеркнуть, сумма двух преобразований T,U:Rn→Rm представляет собой еще одно преобразование, называемое T+U; его значение на входном векторе x является суммой выходов T и U. Точно так же произведение T на скаляр c является другим преобразованием, называемым cT; его значением на входном векторе x является вектор c·T(x).

Пример (функции одной переменной)

В одном из приведенных выше свойств мы использовали 0 для обозначения преобразования Rn→Rm, которое равно нулю для каждого входного вектора: 0(x)=0 для всех x. Это называется нулевым преобразованием .

Приведем теперь аналогичные операции для матриц.

Определение

• Сумма двух матриц размера m×n представляет собой матрицу, полученную суммированием элементов A и B по отдельности:

  Ka11a12a13a21a22a23L+Kb11b12b13b21b22b23L=Ka11+b11a12+b12a13+b13a21+b21a22+b22a23+b23L

  Другими словами, элемент i,j матрицы A+B является суммой элементов i,j матрицы A и B. Обратите внимание, что сложение матриц определяется только тогда, когда обе матрицы имеют одинаковый размер.

• Скалярное произведение скаляра c на матрицу A получается масштабированием всех элементов A на c:

  cKa11a12a13a21a22a23L=Kca11ca12ca13ca21ca22ca23L

  Другими словами, i,j элемент cA равен c раз i,j элементу A.

Факт

Пусть T,U:Rn→Rm — линейные преобразования со стандартными матрицами A, B соответственно, и пусть c — скаляр.

• Стандартная матрица для T+U — A+B.
• Стандартной матрицей для cT является cA.

Ввиду вышеизложенного следующие свойства являются следствием соответствующих свойств преобразований. Они также легко проверяются непосредственно из определений.

В одном из приведенных выше свойств мы использовали 0 для обозначения матрицы размера m×n, все элементы которой равны нулю. Это стандартная матрица нулевого преобразования, она называется нулевой матрицей .

Мы также можем комбинировать сложение и скалярное умножение матриц с умножением матриц. Поскольку умножение матриц соответствует композиции преобразований (теорема), следующие свойства являются следствием соответствующих свойств преобразований.

Большинство приведенных выше свойств легко проверить непосредственно из определений. Однако свойство ассоциативности (AB)C=A(BC) таковым не является (попробуйте!). Гораздо проще доказать, связав умножение матриц с композицией преобразований и используя тот очевидный факт, что композиция преобразований ассоциативна.

Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)

3Blue1Brown — Умножение матриц как композиция

Опубликовано 8 августа 2016 г. 0026 Урок Гранта Сандерсона

Адаптация текста by River Way

Исходный код

«По моему опыту, доказательства с использованием матриц можно сократить на 50%, если матрицы выбросить».

\qquad — Эмиль Артин

Резюме

В предыдущем уроке мы показали, что линейные преобразования — это просто функции с векторами в качестве входных данных и векторами в качестве выходных данных. Однако часто удобнее думать о линейных преобразованиях как о перемещении пространства таким образом, чтобы линии сетки оставались параллельными и равномерно расположенными.

Полноту преобразования можно определить по месту расположения базисных векторов после преобразования, формирующих столбцы матрицы. Чтобы найти, куда попадает любой произвольный вектор после преобразования, существует операция, называемая умножением матрицы на вектор. Вот вычисление для двумерной матрицы и вектора:

[abcd][xy]=x[ac]+y[bd]=[ax+bycx+dy]\begin{bmatrix} \color{green}a & \color{red}b \\ \color{green }c & \color{red}d \end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} = x\begin{bmatrix}\color{green}a\\ \color{green}c\ end{bmatrix} +y\begin{bmatrix}\color{red}b\\ \color{red}d\end{bmatrix} = \begin{bmatrix} \color{green}a\color{black}x+\color {red}b\color{black}y \\ \color{green}c\color{black}x+\color{red}d\color{black}y \end{bmatrix}[ac​bd​][xy​ ]=x[ac​]+y[bd​]=[ax+bycx+dy​]

в конечном итоге заканчивается на [−10]\begin{bmatrix}-1\\0\end{bmatrix}[−10​], так что сделайте это вторым столбцом матрицы. Эта новая матрица фиксирует общий эффект применения вращения, а затем сдвига, но как одно действие, а не два последовательных.

Композиция — это умножение

Вот один из способов представить эту новую матрицу. Если бы вы взяли какой-то вектор и прокачали его через вращение, а затем сдвиг, долгий путь вычислить, где он приземлится, сначала умножив слева на матрицу вращения, а затем умножив результат слева на матрицу сдвига. Это, в численном выражении, то, что это означает , чтобы применить вращение, а затем сдвиг к заданному вектору. Но все, что вы получите, должно быть таким же, как простое умножение этой новой матрицы композиции, которую мы нашли, на вектор, независимо от того, какой вектор вы выбрали, поскольку предполагается, что эта новая матрица захватывает тот же общий эффект, что и действие вращения, затем сдвига.

Основываясь на том, как все здесь записано, я думаю, что будет разумно назвать эту новую матрицу произведением двух исходных матриц, не так ли?

[1101]⏟Сдвиг [0−110]⏟Вращение=[1−110]⏟Композиция\цвет{фиолетовый} \underbrace{ \begin{bmatrix}1&1\\0&1\end{bmatrix} }_{\large \ text{Сдвиг}} \ \color{оранжевый} \underbrace{ \begin{bmatrix}0&-1\\1&0\end{bmatrix} }_{\large \text{Вращение}} \color{black} = \color{ красный} \underbrace{ \begin{bmatrix}1&-1\\1&0\end{bmatrix} }_{\large \text{Композиция}}Сдвиг

[10​11​]​​​Вращение

[01​−10​]​​= Композиция

[11​−10​]​​

Мы можем подумать о том, как вычислить это произведение в более общем виде, просто мгновение, но легко заблудиться в лесу цифр. Всегда помните, что такое умножение двух матриц имеет геометрический смысл применения одного преобразования за другим.

Странно то, что здесь мы читаем справа налево. Сначала вы применяете преобразование, представленное матрицей справа, затем применяете преобразование, представленное матрицей слева. Это проистекает из обозначения функций, поскольку мы пишем функции слева от переменной, поэтому композиция всегда должна читаться справа налево. Хорошие новости для читателей на иврите и плохие новости для всех нас.

f(g(x)) Читать справа налево ←[1101]⏟Сдвиг [0−110]⏟Rotation=[1−110]⏟Composition\begin{align*} &\qquad f(g(x)) \\ &\underleftarrow{\text{Читать справа налево}} \\ &\color{purple} \underbrace{ \begin{bmatrix}1&1\\0&1\end{bmatrix} }_{\large\text{Сдвиг} } \ \color{orange} \underbrace{ \begin{bmatrix}0&-1\\1&0\end{bmatrix} }_{\large\text{Rotation}} \color{black} = \color{red} \underbrace { \begin{bmatrix}1&-1\\1&0\end{bmatrix} }_{\large\text{Композиция}} \end{align*}​f(g(x))

Чтение справа налево Сдвиг

[10​11​]​​Вращение

[01​−10​]​​= Композиция

[11​−10​]​​

Вычисление новой матрицы

Давайте посмотрим на другой пример. Есть две матрицы M1M_1M1​ и M2M_2M2​, которые выполняют разные преобразования:

Суммарный эффект от применения M1M1M1, затем M2M2M2 дает новое преобразование, поэтому давайте найдем его матрицу.

Но давайте посмотрим, сможем ли мы сделать это без каких-либо изображений, а вместо этого просто используя числовые элементы в каждой матрице. 9​))​=[01​20][11​−20][01​]=−2[01​]+0[20​]=[0−2​]​

Умножение этих двух матриц дает [0210][1−210]=?\begin{bmatrix}0&2\\1&0\end{bmatrix}\begin{bmatrix}1&-2\\1&0\end{bmatrix}=?[01​20​][11 ​−20​]=?

[02−21]\begin{bmatrix}0&2\\-2&1\end{bmatrix}[0−2​21​]

[201−2]\begin{bmatrix}2&0\\1&-2\ end{bmatrix}[21​0−2​]

[−2102]\begin{bmatrix}-2&1\\0&2\end{bmatrix}[−20​12​]

[1−220]\begin {bmatrix}1&-2\\2&0\end{bmatrix}[12​−20​]

Общая форма

Давайте повторим тот же процесс еще раз, но на этот раз записи будут переменными в каждой матрице, просто чтобы показать, что один и тот же ход рассуждений работает для любых матриц. Это более тяжелый символ и потребует больше места, но это должно удовлетворить любого, кто ранее учился матричному умножению традиционным способом.

[abcd]⏟M2 [efgh]⏟M1=[????]⏟M2M1\color{purple} \ underbrace{ \begin{bmatrix}a&b\\c&d\end{bmatrix} }_{\large M_2} \ \color{orange} \underbrace{ \begin{bmatrix}e&f\\g&h\end{bmatrix} }_{\large M_1} \color{black} = \color{red} \underbrace{ \begin{bmatrix}? &?\\?&?\end{bmatrix} }_{\large M_2M_1}M2​ 9заканчивается после применения второго преобразования. Таким образом, первый столбец матрицы произведения всегда будет равен левой матрице, умноженной на первый столбец правой матрицы.

[abcd][eg]=e[ac]+g[bd]=[ae+bgce+dg]\color{purple} \begin{bmatrix}a&b\\c&d\end{bmatrix} \color{orange} \begin{bmatrix}e\\g\end{bmatrix} \color{black} = \color{orange} e \color{purple} \begin{bmatrix}a\\c\end{bmatrix} \color{black} + \color{orange} g \color{purple} \begin{bmatrix}b\\d\end{bmatrix} \color{black} = \begin{bmatrix} \color{purple} a \color{orange} e \ color{black} + \color{purple} b \color{orange} g \\ \color{purple} c \color{orange} e \color{black} + \color{purple} d \color{orange} g \ end{bmatrix}[ac​bd​][eg​]=e[ac​]+g[bd​]=[ae+bgce+dg​] 9и, следовательно, второй столбец матрицы продукта.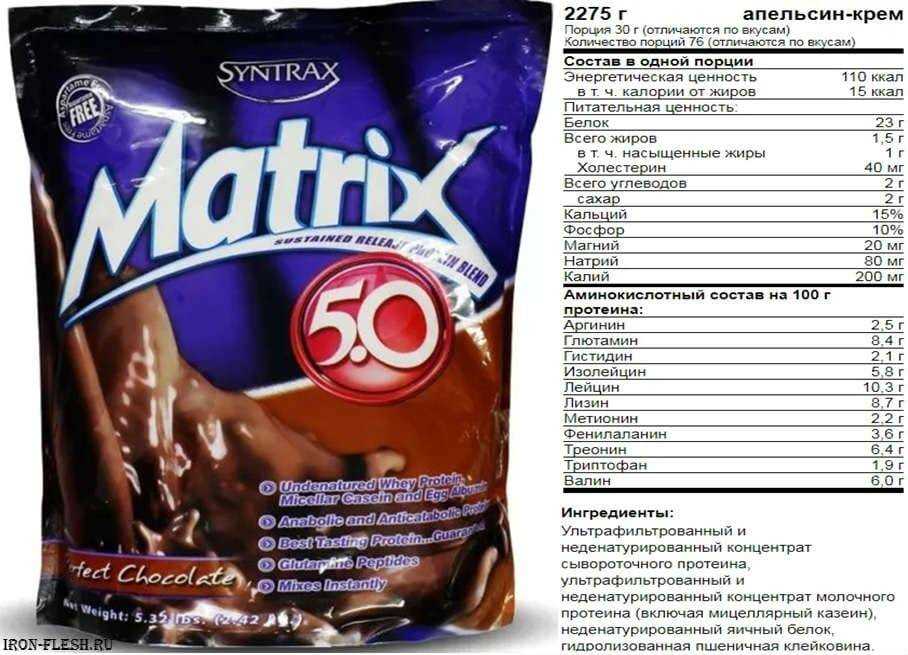

[abcd][fh]=f[ac]+h[bd]=[af+bhcf+dh]\color{purple} \begin{bmatrix}a&b\\c&d\end{bmatrix} \color{orange} \begin{bmatrix}f\\h\end{bmatrix} \color{black} = \color{orange} f \color{purple} \begin{bmatrix}a\\c\end{bmatrix} \color{black} + \color{orange} h \color{purple} \begin{bmatrix}b\\d\end{bmatrix} \color{black} = \begin{bmatrix} \color{purple} a \color{orange} f \ color{black} + \color{purple} b \color{orange} h \\ \color{purple} c \color{orange} f \color{black} + \color{purple} d \color{orange} h \ end{bmatrix}[ac​bd​][fh​]=f[ac​]+h[bd​]=[af+bhcf+dh​]

Обычно эту формулу учат как нечто, что нужно запомнить, наряду с определенным алгоритмическим процессом для ее запоминания.

[abcd]⏟M2 [efgh]⏟M1=[ae+bgaf+bhce+dgcf+dh]⏟M2M1\color{purple} \underbrace{ \begin{bmatrix}a&b\\c&d\end{bmatrix} }_ {\ large M_2} ​​\ \ color {orange} \ underbrace { \ begin {bmatrix} e&f \\ g&h \ end {bmatrix} } _ {\ large M_1} \ color {black} = \ color {red} \ underbrace { \ begin{bmatrix} \color{purple} a \color{orange} e \color{black} + \color{purple} b \color{orange} g & \color{purple} a \color{orange} f \color{ черный} + \color{purple} b \color{orange} h \\ \color{purple} c \color{orange} e \color{black} + \color{purple} d \color{orange} g & \color {purple} c \color{orange} f \color{black} + \color{purple} d \color{orange} h \end{bmatrix} }_{\large M_2M_1}M2​

[ac​bd​]​​M1​

[eg​fh​]​=M2​M1​

[ae+bgce+dg​af+bhcf+dh​]​​

Умножение этих двух матрицы дают [−3125][537−3]=?\begin{bmatrix}-3&1\\2&5\end{bmatrix}\begin{bmatrix}5&3\\7&-3\end{bmatrix}=?[−32​ 15​][57​3−3​]=?

[45−9−8−12]\begin{bmatrix}45&-9\\-8&-12\end{bmatrix}[45−8​−9−12​]

[−12−8− 945]\begin{bmatrix}-12&-8\\-9&45\end{bmatrix}[−12−9−845​]

[−945−12−8]\begin{bmatrix}-9&45\\- 12&-8\end{bmatrix}[−9−12​45−8​]

[−8−1245−9]\begin{bmatrix}-8&-12\\45&-9\end{bmatrix}[−845​−12−9​]

Я действительно считаю, что прежде чем запоминать этот процесс, вы должны привыкнуть думать о том, что на самом деле представляет собой умножение матриц: применение одного преобразования за другим. Поверьте мне, это даст вам концептуальную основу, облегчающую понимание свойств матричного умножения.

Некоммутативность

Вот важный вопрос: имеет ли значение, в каком порядке мы располагаем две матрицы? 9\circ90∘ вращение.

Общий эффект совсем другой, так что может показаться, что порядок имеет значение! Думая с точки зрения преобразований, это то, что вы можете делать в своей голове, визуализируя, без необходимости умножения матриц!

При умножении этих двух матриц [0-110][-200-2]=?[-200-2][0-110]\begin{bmatrix}0&-1\\1&0\end{bmatrix}\begin{ bmatrix}-2&0\\0&-2\end{bmatrix}\stackrel{?}{=}\begin{bmatrix}-2&0\\0&-2\end{bmatrix}\begin{bmatrix}0&-1\\1&0 \end{bmatrix}[01​−10][−20​0−2​]=?[−20​0−2][01​−10​]

Да, матрицы коммутируют.

Нет, матрицы не коммутируют.

Ассоциативность. Это означает, что если у вас есть три матрицы, A, B и C, и вы умножаете их все, не имеет значения, вычисляете ли вы сначала A, умноженное на B, а затем умножаете результат на C, или если вы сначала умножаете B на C, а затем умножаете результат по матрице A слева.